No setor florestal o fogo é uma questão recorrente e preocupante. Utilizar um índice de risco ou perigo de incêndio ajuda, no mínimo, no planejamento e no alerta para quem mora no entorno de maciços florestais como parques, hortos e plantios florestais.

A Fórmula de Monte Alegre (FMA) é um índice bastante simples, foi proposta em 1972 por Soares (1972) e utiliza apenas a umidade relativa do ar às 13h e a precipitação para calcular o risco de incêndio. É um índice que possui 5 classes de risco e é cumulativo, portanto precisa ser calculado todos os dias.

O objetivo deste post é implementar a FMA utilizando dados de 1988 à 2017 da estação meteorológica convencional da ESALQ em Piracicaba.

if (!require("pacman")) install.packages("pacman")
pacman::p_load(readr, dplyr, tidyr, forcats, lubridate, ggplot2, ggridges)

base <- read_csv2(
  "https://raw.githubusercontent.com/italocegatta/italocegatta.github.io_source/master/content/dados/posto_esalq_dia.csv",
  col_types = cols(.default = col_number(), data = col_character())
)

base

## # A tibble: 10,961 x 3
##    data         ppt ur_med
##    <chr>      <dbl>  <dbl>
##  1 01/01/1988   0       62
##  2 02/01/1988   0       65
##  3 03/01/1988   0       65
##  4 04/01/1988   0       69
##  5 05/01/1988  33.9     74
##  6 06/01/1988  66       90
##  7 07/01/1988   0       78
##  8 08/01/1988   0.5     88
##  9 09/01/1988  17.1     83
## 10 10/01/1988   7.8     83
## # ... with 10,951 more rows

O primeiro passo é estimar a umidade relativa às 13h, uma vez que é este valor que a FMA considera para o cálculo. Utilizaremos a equação ajustada por Alvares et al. (2014).

base_fma <- base %>%
  mutate(
    data = dmy(data),
    ur13 = (8.77 * exp(0.024 * ur_med)) - 2.943
  ) %>% 
  select(data, ppt, ur13)

base_fma

## # A tibble: 10,961 x 3
##    data         ppt  ur13
##    <date>     <dbl> <dbl>
##  1 1988-01-01   0    35.9
##  2 1988-01-02   0    38.8
##  3 1988-01-03   0    38.8
##  4 1988-01-04   0    43.0
##  5 1988-01-05  33.9  48.9
##  6 1988-01-06  66    73.1
##  7 1988-01-07   0    54.1
##  8 1988-01-08   0.5  69.5
##  9 1988-01-09  17.1  61.3
## 10 1988-01-10   7.8  61.3
## # ... with 10,951 more rows

Agora vamos fazer uma breve análise dos dados brutos. Começando pela chuva, podemos calcular o número médio de dias de chuva forte e fraca neste período. Entre julho e agosto há poucas chuvas em Piracicaba e isso já sugere que neste período o risco de incêndio deve ser alto.

base_fma %>%
  mutate(ano = year(data), mes = month(data)) %>% 
  mutate(
    d_1 = ifelse(ppt > 1 & ppt <= 5, 1, 0),
    d_5 = ifelse(ppt > 5 , 1, 0)
  ) %>% 
  group_by(ano, mes) %>% 
  summarise_at(vars(d_1, d_5), sum, na.rm = TRUE) %>% 
  group_by(mes) %>% 
  summarise_at(vars(d_1, d_5), ~round(mean(.))) %>% 
  ungroup() %>% 
  rename(`<5` = d_1, `>5` = d_5) %>% 
  gather(nivel, d_chuva, `<5`:`>5`) %>% 
  mutate(
    d_chuva = ifelse(d_chuva == 0, NA, d_chuva),
    nivel = fct_relevel(nivel, "<5" , ">5")
  ) %>% 
  ggplot(aes(mes, d_chuva, fill = nivel)) +
    geom_col(alpha = 0.8) +
    labs(
      x = "Mês do ano",
      y = "Nº de dias de chuva (#)",
      fill = NULL
    ) +
    scale_x_continuous(breaks = 1:12, labels = format(ISOdate(2000, 1:12, 1), "%b")) +
    scale_y_continuous(breaks = seq(0, 30, 2), expand = expand_scale(mult = c(0.01, .1))) +
    scale_fill_manual(
      values = c("#4292c6", "#084594"),
      labels = c("Chuva fraca (<5 mm)","Chuva forte (>5 mm)")
    ) +
    theme_bw(16) +
    theme(legend.position = "top", panel.grid.minor.x = element_blank())

Olhando para a distribuição da umidade relativa em cada mês, podemos ver que em junho a mediana ainda está próximo dos 50% de umidade. E só em julho que os dias mais secos começam a ter mais frequência e essa tendência aumenta até setembro, depois retorna gradativamente até a mediana de 57% de umidade em dezembro.

base_fma %>% 
  filter(!is.na(ur13)) %>% 
  mutate(mes = factor(month(data))) %>% 
  ggplot(aes(ur13, mes)) +
    geom_density_ridges(quantile_lines = TRUE, quantiles = 2, fill = "#016c59", alpha = 0.9) +
    labs(x = "Umidade Relativa às 13h (%)", y = "Mês do ano") +
    scale_x_continuous(breaks = seq(10, 100, 10)) +
    scale_y_discrete(labels = format(ISOdate(2000, 1:12, 1), "%b")) +
    theme_bw(16)

Sobre a Fórmula de Monte Alegre, o contexto que motivou seu desenvolvimento foi bastante trágico. Em 1963 um grande incêndio atingiu o estado do Paraná, com centenas de mortes e cerca de 2 milhões de hectares de florestas queimadas. Em 1972 o Professor Ronaldo Soares, da UFPR, defendeu sua tese de mestrado propondo a Fórmula de Monte Alegre com base em registros de incêndios florestais coletados a partir de 1965 na fazenda Monte Alegre (Klabin), em Telêmaco Borba-PR.

A cálculo do índice é bastante simples, basta calcular o valor FMA do dia corrente e somar com o valor do dia anterior. O FMA é calculado através da seguinte expressão:

$FMA = \sum_{i=1}^n \frac{100}{URi_{13h}}$

Entretanto é preciso aplicar restrições ao valor FMA de acordo com a chuva do dia, seguindo estes parâmetros:

Precipitação	Restrição
< 2,5	Nenhuma
2,5 - 4,9	0,7 * FMAi-1 + FMAi
5,0 - 9,9	0,4 * FMAi-1 + FMAi
10,0 - 12,9	0,2 * FMAi-1 + FMAi
> 12,9	Interromper o cálculo anterior (FMAi = 0) e começar novo cálculo no dia seguinte

O resultado do índice é apresentado com frequência na forma de classes de risco, obedecendo estes limites:

FMA	Grau de perigo
0 - 1,0	Nulo
1,1 - 3,0	Pequeno
3,1 - 8,0	Médio
8,1 – 20,0	Alto
> 20,0	Muito alto

Vamos agora declara as funções que vão calcular o FMA e atribuir as classes de risco aos nossos dados.

fma <- function(data, ur, ppt) {
  
  # testa se os dados estão ordenados
  if (any(data != sort(data))) {
    stop("data precisa estar em ordem crescente")
  }

  # cria o vetor de resultado  
  n <- length(ur)
  fma_vec <- rep(NA_real_, n)
  
  for (i in seq_len(n)) {
    
    # primeiro valor eh 0   
    if (i == 1) {
      fma_vec[i] <- 0
      next()
    }
    
    # se dia anterior nao tem informacao, valor eh 0
    if (is.na(ur[i - 1])) {
      fma_vec[i] <- 0
      next()
    }
    
    # aplica restricoes da chuva
    fma_vec[i] <- case_when(
      ppt[i] < 2.5 ~ (100 / ur[i]) + fma_vec[i - 1] * 1 ,
      ppt[i] >= 2.5 & ppt[i] < 5  ~ (100 / ur[i]) + fma_vec[i - 1] * 0.7,
      ppt[i] >= 5   & ppt[i] < 10 ~ (100 / ur[i]) + fma_vec[i - 1] * 0.4,
      ppt[i] >= 10  & ppt[i] < 13 ~ (100 / ur[i]) + fma_vec[i - 1] * 0.2,
      ppt[i] >= 13 ~ 0
    )
  }
  
  fma_vec
}

fma_classe <- function(fma, limites = c(1, 3, 8, 20)) {
  
  classe <- case_when(
    fma <= 1 ~ "Nulo",
    fma > 1 & fma <= 3 ~"Pequeno",
    fma > 3 & fma <= 8 ~ "Médio",
    fma > 8 & fma <= 20 ~ "Alto",
    fma > 20 ~ "Muito Alto"
  )
  
  factor(classe, levels = c("Nulo", "Pequeno", "Médio", "Alto", "Muito Alto"))
}

Seguindo para o cálculo do índice, vamos criar um novo data frame com o valor FMA e as classes de riscos utilizando as funções que acabamos de criar.

dados_fma <- base_fma %>% 
  mutate(
    fma = fma(data, ur13, ppt),
    risco = fma_classe(fma)
  )

dados_fma

## # A tibble: 10,961 x 5
##    data         ppt  ur13   fma risco  
##    <date>     <dbl> <dbl> <dbl> <fct>  
##  1 1988-01-01   0    35.9  0    Nulo   
##  2 1988-01-02   0    38.8  2.58 Pequeno
##  3 1988-01-03   0    38.8  5.16 Médio  
##  4 1988-01-04   0    43.0  7.48 Médio  
##  5 1988-01-05  33.9  48.9  0    Nulo   
##  6 1988-01-06  66    73.1  0    Nulo   
##  7 1988-01-07   0    54.1  1.85 Pequeno
##  8 1988-01-08   0.5  69.5  3.29 Médio  
##  9 1988-01-09  17.1  61.3  0    Nulo   
## 10 1988-01-10   7.8  61.3  1.63 Pequeno
## # ... with 10,951 more rows

A primeira abordagem que quero mostrar é a evolução do valor FMA ao longo do ano. Considerando o dia do ano ou dia juliano, podemos ver a evolução do valor FMA devido á ausência de chuvas fortes. O máximo dessa “corrida” de risco vai até próximo do dia 290, que corresponde ao meio de outubro.

dados_fma %>% 
  mutate(
    ano = year(data),
    dia_ano = yday(data)
  ) %>% 
  ggplot(aes(dia_ano, factor(ano), fill = fma)) +
  geom_tile() +
  labs(x = "Dia do ano", y = "Ano", fill = "FMA") +
  scale_fill_viridis_c(option = "viridis") +
  scale_x_continuous(breaks = seq(20, 360, 20), expand = c(0, 0)) +
  theme_bw()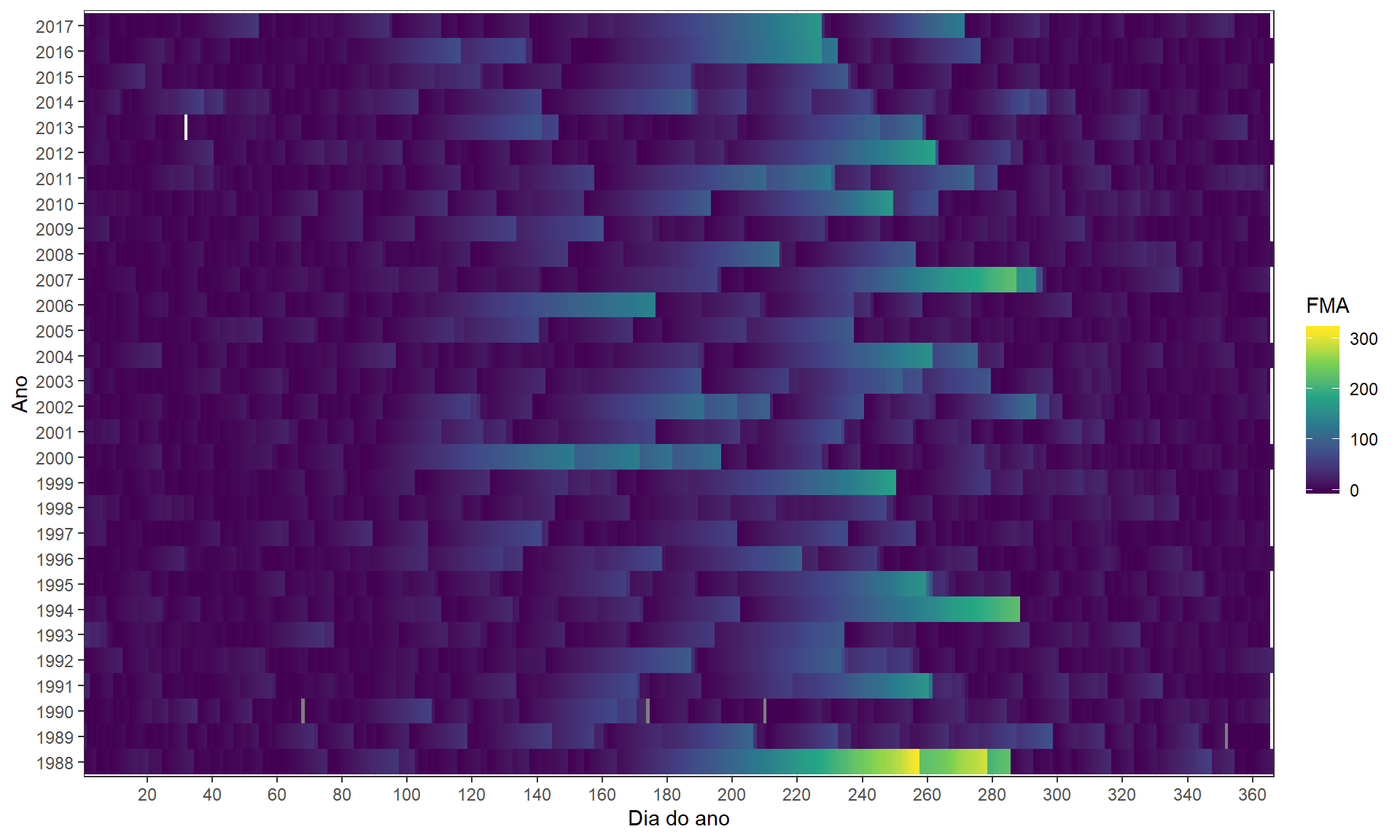

Calculando a frequência das classes dentro de cada ano, podemos ver que predomina o risco Muito Alto, seguido do risco Alto. O risco nulo, ocorre em aproximadamente 10% dos dias do ano.

dados_fma  %>% 
  filter(!is.na(risco)) %>% 
  group_by(ano = year(data), risco) %>% 
  tally() %>% 
  ggplot(aes(ano, n, fill = risco)) +
  geom_col(position = "fill", alpha = 0.8) +
  labs(x = "Ano", y = "Frequência", fill = "Risco") +
  scale_y_continuous(breaks = seq(0.1, 1, 0.1), labels = scales::percent) +
  scale_fill_brewer(palette = "Spectral", direction = -1) +
  theme_bw(16)

Olhando para a frequência de risco dentro dos meses, fica claro o maior risco próximo do mês de agosto, como sugeriram os gráficos de frequências de chuva e umidade relativa.

dados_fma  %>% 
  filter(!is.na(risco)) %>% 
  group_by(mes = month(data), risco) %>% 
  tally() %>% 
  ggplot(aes(mes, n, fill = risco)) +
  geom_col(position = "fill", alpha = 0.8) +
  labs(x = "Mês do ano", y = "Frequência", fill = "Risco") +
  scale_x_continuous(breaks = 1:12, labels = format(ISOdate(2000, 1:12, 1), "%b")) +
  scale_y_continuous(labels = scales::percent) +
  scale_fill_brewer(palette = "Spectral", direction = -1) +
  theme_bw(16)

Bom, de maneira geral os gráficos não mostraram muita coisa nova. Todo mundo sabe que nos meses mais secos do ano o risco de incêndio é maior. De fato, o índice apenas dá um respaldo quantitativo para o senso comum. Uma vez calculado o índice, é possível confrontar com dados reais de incêndios e propor novos valores para as classes de risco com o objetivo de deixá-lo mais assertivo para uma certa região.

Caso tenha alguma dúvida ou sugestão sobre o post, fique à vontade para fazer um comentário ou me contatar por E-mail.

sessioninfo::session_info(c("readr", "dplyr", "ggplot2", "tidyr", "forcats", "lubridate", "ggridges"))

## - Session info ----------------------------------------------------------
##  setting  value                       
##  version  R version 3.5.3 (2019-03-11)
##  os       Windows 10 x64              
##  system   x86_64, mingw32             
##  ui       RTerm                       
##  language (EN)                        
##  collate  Portuguese_Brazil.1252      
##  ctype    Portuguese_Brazil.1252      
##  tz       America/Sao_Paulo           
##  date     2019-08-25                  
## 
## - Packages --------------------------------------------------------------
##  package      * version  date       lib source        
##  assertthat     0.2.1    2019-03-21 [1] CRAN (R 3.5.3)
##  backports      1.1.4    2019-04-10 [1] CRAN (R 3.5.3)
##  BH             1.69.0-1 2019-01-07 [1] CRAN (R 3.5.2)
##  cli            1.1.0    2019-03-19 [1] CRAN (R 3.5.3)
##  clipr          0.7.0    2019-07-23 [1] CRAN (R 3.5.3)
##  colorspace     1.4-1    2019-03-18 [1] CRAN (R 3.5.3)
##  crayon         1.3.4    2017-09-16 [1] CRAN (R 3.5.1)
##  digest         0.6.20   2019-07-04 [1] CRAN (R 3.5.3)
##  dplyr        * 0.8.3    2019-07-04 [1] CRAN (R 3.5.3)
##  ellipsis       0.2.0.1  2019-07-02 [1] CRAN (R 3.5.3)
##  fansi          0.4.0    2018-10-05 [1] CRAN (R 3.5.1)
##  forcats      * 0.4.0    2019-02-17 [1] CRAN (R 3.5.2)
##  ggplot2      * 3.2.1    2019-08-10 [1] CRAN (R 3.5.3)
##  ggridges     * 0.5.1    2018-09-27 [1] CRAN (R 3.5.2)
##  glue           1.3.1    2019-03-12 [1] CRAN (R 3.5.3)
##  gtable         0.3.0    2019-03-25 [1] CRAN (R 3.5.3)
##  hms            0.5.0    2019-07-09 [1] CRAN (R 3.5.3)
##  labeling       0.3      2014-08-23 [1] CRAN (R 3.5.0)
##  lattice        0.20-38  2018-11-04 [2] CRAN (R 3.5.3)
##  lazyeval       0.2.2    2019-03-15 [1] CRAN (R 3.5.3)
##  lubridate    * 1.7.4    2018-04-11 [1] CRAN (R 3.5.1)
##  magrittr       1.5      2014-11-22 [1] CRAN (R 3.5.1)
##  MASS           7.3-51.1 2018-11-01 [2] CRAN (R 3.5.3)
##  Matrix         1.2-17   2019-03-22 [1] CRAN (R 3.5.3)
##  mgcv           1.8-28   2019-03-21 [1] CRAN (R 3.5.3)
##  munsell        0.5.0    2018-06-12 [1] CRAN (R 3.5.1)
##  nlme           3.1-137  2018-04-07 [2] CRAN (R 3.5.3)
##  pillar         1.4.2    2019-06-29 [1] CRAN (R 3.5.3)
##  pkgconfig      2.0.2    2018-08-16 [1] CRAN (R 3.5.1)
##  plogr          0.2.0    2018-03-25 [1] CRAN (R 3.5.1)
##  plyr           1.8.4    2016-06-08 [1] CRAN (R 3.5.1)
##  purrr          0.3.2    2019-03-15 [1] CRAN (R 3.5.3)
##  R6             2.4.0    2019-02-14 [1] CRAN (R 3.5.2)
##  RColorBrewer   1.1-2    2014-12-07 [1] CRAN (R 3.5.0)
##  Rcpp           1.0.2    2019-07-25 [1] CRAN (R 3.5.3)
##  readr        * 1.3.1    2018-12-21 [1] CRAN (R 3.5.2)
##  reshape2       1.4.3    2017-12-11 [1] CRAN (R 3.5.1)
##  rlang          0.4.0    2019-06-25 [1] CRAN (R 3.5.3)
##  scales         1.0.0    2018-08-09 [1] CRAN (R 3.5.1)
##  stringi        1.4.3    2019-03-12 [1] CRAN (R 3.5.3)
##  stringr        1.4.0    2019-02-10 [1] CRAN (R 3.5.2)
##  tibble         2.1.3    2019-06-06 [1] CRAN (R 3.5.3)
##  tidyr        * 0.8.3    2019-03-01 [1] CRAN (R 3.5.3)
##  tidyselect     0.2.5    2018-10-11 [1] CRAN (R 3.5.1)
##  utf8           1.1.4    2018-05-24 [1] CRAN (R 3.5.1)
##  vctrs          0.2.0    2019-07-05 [1] CRAN (R 3.5.3)
##  viridisLite    0.3.0    2018-02-01 [1] CRAN (R 3.5.1)
##  withr          2.1.2    2018-03-15 [1] CRAN (R 3.5.1)
##  zeallot        0.1.0    2018-01-28 [1] CRAN (R 3.5.2)
## 
## [1] C:/Users/Italo/Documents/R/win-library/3.5
## [2] C:/Program Files/R/R-3.5.3/library

Referências

Alvares, Clayton Alcarde, Italo Ramos Cegatta, Lucas Augusto Abra Vieira, Rafaela de Freitas Pavani, Eduardo Moré Mattos, Paulo Cesar Sentelhas, José Luiz Stape, and Ronaldo Viana Soares. 2014. “Perigo de Incêndio Florestal: Aplicação Da Fórmula de Monte Alegre E Avaliação Do Histórico Para Piracicaba, Sp.” Scientia Forestalis, Piracicaba 42 (104): 511–22.

Soares, Ronaldo Viana. 1972. “Determinação de Um ı́ndice de Perigo de Incêndio Para a Região Centro Paranaense, Brasil. Turrialba, Costa Rica, Catie/Iica,. 72 P.” PhD thesis, Tese de Mestrado.

Risco de incêndio pela Fórmula de Monte Alegre

Referências

Ítalo Cegatta

Risco de incêndio pela Fórmula de Monte Alegre

Referências

Ítalo Cegatta

O quão popular é o seu nome?

Risco de incêndio pela Fórmula de Monte Alegre

Qual Estado tem mais pau-rodado?

100 anos do posto meteorológico da ESALQ

Engenheiro Florestal ou Cientista de Dados?

Como um cientista de dados pesquisa o carro que quer comprar?

Gráficos com dimensão espacial e temporal

Interpolação pelo inverso do quadrado da distância

Download automático de imagens MODIS

Índice de uniformidade (PV50)